Lab 5: Regression Analysis

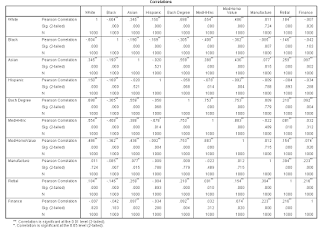
Part 1

A city is looking for an answer to an interesting question they have been trying to figure out and were not 100% sure how to go about it. Using data for Town X a local newspaper made the claim that as the number of students who get free lunches increases so does the crime rate for the designated areas. 

Using Regression Analysis in SPSS we can test to see if there is any type of relationship between the two data sets that the newspaper claimed to be true. For this test we were given data sets for multiple areas of town X, this data include crime rate per 100,000 people and the percentage of students who were on the free lunch program. I decided to use the crime rate as the dependent variable and the percentage of students who receive free lunches as the independent variable. I chose to do it this way because we are testing to see if the crime rate increases as more students receive free lunches. 

Therefore for this test scenario, the crime rate is dependent upon how many students are receiving the free lunches at school. An argument could be made to flip the two variable and make the crime rate the independent variable and say the number of students who get free lunches is dependent upon the crime rate, but for the sake of this study I felt the originally mentioned way made the most sense.

I initially created a scatter plot in Microsoft Excel to get a general idea if there was any type of trend line associated with the data before I ran the data through SPSS (figure 1). I found a small linear relationship (based just on looking at it) and also found one set of data that seemed way out of place, will address that issue later.

Figure 1: Chart created using Microsoft Excel showing the trend line

After performing regression analysis in SPSS I found an r² value of .173 at a significance level of 0.005 (figure 2). With this data I can reject the null hypothesis because there is a linear relationship between students who receive free lunches and the crime rate. The town then had a new area which has 23.5% of students receiving free lunches and wanted to know what the potential crime rate could be. Using the equation Y = 21.819 + 1.685(x) and inserting 23.5 in for X we get a crime rate of 61.4165 per 100,000 people. When asked how confident I am about the data I cannot give a full certainty answer because the graphs only can account for about 17% of the data.

Figure 2: The data gathered from running regression analysis on the crime/lunch data

As mentioned before there was one outlier in the data. Curious to what the data would look like I deleted it and ran the regression analysis again using the same dependent and independent variables as before. After running the test the r² value nearly doubled to 0.389. The crime rate per 100,000 people also declined to 60.816 when the students who receive free lunches is at 23.5%. If we chose this data set instead of the original data we can be much more confident with our answer because the model can explain almost 40% of the data. The equation used for this was Y = 31.77 + 1.236(x) where X was 23.5.

Part 2

Methods

The second part of this assignment is to analyze and interpret any statistical patterns amongst the data for UW School Students out of the 72 Wisconsin Counties. This data is only looking at students from the State of Wisconsin, a student is considered from Wisconsin if their permanent address is located within the state boundary. For this section we will be using ESRI Arc Map and SPSS software to compile different numerical features for the data set.

I decided to use the University of Wisconsin- Oshkosh as my other school to test, along with the University of Wisconsin-Eau Claire. Using the excel spread sheet we were given, it contained information on every county including, population, people under the age of 24, people who have Bachelor’s Degrees, distance from the center of the county to the respected university, median house hold income and how many students from the county attend the respected University.

The first step was to normalize the county population for both schools. This was done by created two additional columns in the excel spreadsheet, one for each of the schools. Using the total population of the county and dividing it by the distance from either UWEC or UWO. We were tasked with running three independent/dependent variable tests on each of the schools and mapping out those that were significant in ArcMap. For it to be considered significant, we would be rejecting the null hypothesis therefore assuming there is a linear relationship between the two data sets.

The six tests run were (dependent variable is always listed first followed by the independent variable);

1-Number of Students Attending UWEC from the respected counties (EAU) and Population Normalization

2-Number of Students Attending UWO from the respected counties (OSH) and Population Normalization

3-(EAU) and Percentage of People living in each county who hold a bachelor’s degree

4-(OSH) and Percentage of People living in each county who hold a bachelor’s degree

5-(EAU) and Median Household income for the respected County

6-(OSH) and Median Household income for the respected County

Of the 6 hypotheses tested, only one failed to reject the null hypothesis. That one was number 5, I did not find a linear relationship between the Number of Students Attending UWEC from the respected counties and the median household income from the respected county. The other 5 all showed at least some linear relationship and will be broken down further in the results section.

Using the five hypotheses that showed significant linear relationship, we had to map the residuals of the data. Residuals are the distance each data point is above the best fit line. Otherwise stated, it is the distance between the observed and the expected value. So if you had an observed value of 5 for a given point, and the expected value for the same given point was 3, you would have a residual of 2 for that one point.

Instead of having to go through this for each point by hand, SPSS can do it very quickly and also store the value in the database. After running this five times, for each of the hypotheses found significant, save the file as a database and import it into ArcMap.

Once in ArcMap using ordinary least squares regression analysis it will become visible which counties are significantly greater than the mean, or less than. 

Results of the Individual Hypotheses

Hypothesis One: Students Attending the University of Wisconsin-Eau Claire based on Population Distance Normalization

Variables being tested: Number of students attending UWEC from each county and the population distance normalization variable (independent).

R² = 0.945 at a significant level of 0.000

Equation = Y = 8.518 + .124(x)

Data attained from Figure 3

Figure 3: Data calculated in SPSS while running regression analysis

REJECT THE NULL HYPOTHESIS DUE TO LINEAR RELATIONSHIP BETWEEN STUDENTS ATTENDING UWEC AND POPULATION DISTANCE NORMALIZATION.

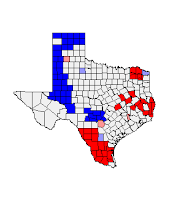
This map shows the Standard Deviation of Students attending the University of Wisconsin-Eau Claire from different counties. The population variable was normalized to by taking the total population from the county and dividing it by the distance the center of the county is from the University. The figure shows one county, Eau Claire County to be over 2.5 standard deviations greater than the mean. There is also one county that is slightly less than 2.5 Standard Deviations above the mean, Chippewa County. These two counties are both over 2 standard deviations above the mean because one they are the closest to the county and two because they contribute a large amount of students to the university, most likely due to its closeness. Other areas we see have above the mean standard deviations of significant levels are the Madison, Wausau and Green Bay areas (Dane, Marathon and Brown County). These counties are significant because of their large populations and for Marathon County, its closeness to UWEC (figure 4)

Figure 4: Standard Deviation Mapping residuals from the first hypothesis 

Hypothesis two: Students attending the University of Wisconsin-Oshkosh Based on Population Distance Normalization

Variables being tested: Number of students attending UWO from each county and the population distance normalization variable (independent).

R² = 0.919 at a significance level of 0.000

Equation = Y = 13.887 + 0.076(x)

Data attained from Figure 5

Figure 5

REJECT THE NULL HYPOTHESIS DUE TO LINEAR RELATIONSHIP BETWEEN STUDENTS ATTENDING UWO AND POPULATION DISTANCE NORMALIZATION

The University of Wisconsin Oshkosh is located in eastern Wisconsin and about in the middle of the eastern portion of the state. The map created shows a few counties above the non-significant (-0.5 – 0.5) range. We see two counties touching Winnebago County that are above the mean standard deviation (Outagamie and Fond du Lac Counties). Four counties not within contact but still provide a large number of people to UWO include Brown, Dane, Milwaukee and Waukesha Counties. Each of these counties have at least one largely populated city which probably contributes to the high number of students attending UWO (Madison, Milwaukee, Green Bay and Waukesha). This test did not show any counties to be below -0.5 standard deviations of the mean suggesting a possible low enrollment mean per county and then a couple outliers such as Milwaukee County which would then make for a large standard deviation (figure 6).

Figure 6

Hypothesis three: Students attending the University of Wisconsin Eau Claire and Percentage of People with Bachelor’s Degrees in Home Counties

Variables being tested: Number of students attending UWEC and Percentage of people with Bachelor’s Degrees in Home Counties (independent variable)

R² = 0.121 at a significance level of 0.003

Equation = Y = -126.472 – 4283.038(x)

Data attained from Figure 7

Figure 7

REJECT THE NULL HYPOTHESIS DUE TO LINEAR RELATIONSHIP BETWEEN STUDENTS ATTENDING UWEC AND THE PERCENTAGE OF PEOPLE IN THE RESPECTED COUNTIES WHO HAVE BACHELOR DEGREES

With this map we see multiple counties with different colors. Again the redder the county the further away, positive direction, the county’s residual is from the expected value or mean. Again we see the Madison and Milwaukee areas to be very high above the expected value. This can again be contributed to larger city status and possibly jobs in the area require a higher form of education. Other counties such as Menominee and Trempealeau Counties are below the standard deviation or expected value, and this could be because in Menominee not many people have Bachelor’s Degrees because it is not needed since they are basically a closed off reserve. Basically when looking at this map, several of the counties in red shades are home to larger cities, while blue are smaller more farm/forested areas, with the exception to Bayfield County (figure 8).

Figure 8

 

Hypothesis four: Students attending the University of Wisconsin Oshkosh and Percentage of People with Bachelor’s Degrees in Home Counties

Variables being tested: Number of students attending UWO and Percentage of people with Bachelor’s Degrees in Home Counties (independent variable)

R² = 0.129 at a significance level of 0.002

Equation = Y = -187.382 + 5733.635(x)
Data attained from Figure 9

Figure 9

 

REJECT THE NULL HYPOTHESIS DUE TO LINEAR RELATIONSHIP BETWEEN STUDENTS ATTENDING UWO AND THE PERCENTAGE OF PEOPLE IN THE RESPECTED COUNTIES WHO HAVE BACHALOR DEGREES

With this map we see multiple counties with different colors. Again the redder the county the further away, positive direction, the county’s residual is from the expected value or mean. Here we see Winnebago and Outagamie Counties to be over 2.5 Standard Deviations above the mean or expect value. Milwaukee and Brown County are in the category right below those two. Several Counties spread out across the state are in the negative standard deviations and this could again contribute to a smaller population or more farm land then built up areas (figure 10).

Figure 10

 

Hypothesis five: Students attending the University of Wisconsin Eau Claire and the relationship it has with the median household income of the respected counties.

Variables being tested: Number of students attending UWEC and median household income in Home Counties (independent variable)

R² = 0.007 at a significance level of 0.104

Equation = Y = -80.928 + 0.006(x)
Data attained from Figure 11

Figure 11

FAIL TO REJECT THE NULL HYPOTHESIS DUE TO NO LINEAR RELATIONSHIP BETWEEN STUDENTS ATTENDING UWEC AND THE MEDIAN HOUSE HOLD INCOME IN THE RESPECTED COUNTIES

Because this data was not considered to be significant at 95% significance level the residuals were not mapped. This being said I did not find a significant enough linear relationship amongst the two variables and therefore failed to reject the null hypothesis.

Hypothesis six: Students attending the University of Wisconsin Oshkosh and the relationship it has with the median household income of the respected counties.

Variables being tested: Number of students attending UWO and median household income in Home Counties (independent variable)

R² = 0.146 at a significance level of 0.001
Equation = Y = -356.693 + 0.015(x)
Data attained from Figure 12

Figure 12

 

REJECT THE NULL HYPOTHESIS DUE TO LINEAR RELATIONSHIP BETWEEN STUDENTS ATTENDING UWO AND THE MEDIAN HOUSE HOLD INCOME IN THE RESPECTED COUNTIES

In the map we see a general split running diagonal across Wisconsin, with the exceptions to Marathon, St. Croix, Pierce and Wood Counties. The counties left of the diagonal line are below the standard deviation, and I believe this may be the case of vastly wooded areas as well as smaller populations where there is not much high income people claiming permanent residence in those locations. In the southeastern and eastern portion of Wisconsin we see most of the red counties in the state. This is meaning they are above the expected value. This could be because of two reasons, one they are in close proximity to Oshkosh and two they have larger cities with largely built up areas that have higher income levels (figure 13).

Figure 13

Discussion

Residuals for each of the 5 hypotheses that rejected the null hypothesis.

When looking at the residual values for the five significant hypotheses we see as the r squared value decreases, or gets closer to zero, the range between the minimum and maximum residual values increases. Along with the increase in range between the two values the standard deviation also increases. Using this information, for example, Image1 has an r² value of 0.945. This is seen as a near perfect line. Then when we look at the minimum value (-291.793) and the maximum residual value (156.910) we see that the range is only 448.703. Now if we take a look at Image6 that had an r² value of only 0.146. We see the minimum residual value (-368.859) and the maximum residual value (1906.635) have a range of 2275.494 and a standard deviation of 265.895. In this lab when it comes to dealing with the residual values and standard deviations, it appears that there is a direct link between the r squared value and the range between the maximum residual value and the minimum residual value.

Image	R2	Minimum Residual Value	Maximum Residual Value	Range	Standard Deviation
Image1	0.945	-291.793	156.910	448.703	52.131
Image2	0.919	-351.387	404.019	755.406	82.036
Image3	0.121	-264.069	1603.142	1867.211	208.129
Image4	0.129	-321.330	1864.982	2186.312	268.627
Image6	0.146	-368.859	1906.635	2275.494	265.895

 Conclusion
There is not a perfect correlation between the r² value and the range of the residuals, but nonetheless there is a pattern relating to higher r² values resulting in smaller ranges. When looking at the table and comparing it to the maps created above, some maps do not contain much dark blue (2.5 negative standard deviations) or bright red (2.5 positive standard deviations) and that may just be because they do not exist.

Image	+/-2.5 Standard Deviations	Minimum Residual Value	Maximum Residual Value
Image1	+/-130.32	-291.793	156.910
Image2	+/-205.09	-351.387	404.019
Image3	+/-520.3225	-264.069	1603.142
Image4	+/-671.5675	-321.330	1864.982
Image6	+/-664.7375	-368.859	1906.635

As the table shows above three of the five images (3,4 and 6) minimum value do not come close to the -2.5 standard deviations value, this is the primary reason to why the maps are so yellow (-0.5 to 0.5 standard deviations) or light blue (-0.5 to -1.5 standard deviations).

Lab 4: Correlation and Spatial Autocorrelation

Correlation

In order to measure if there is any correlation between the distances someone is away from the sound source and the level of the sound measured in decibels (dB) there are tools in both Microsoft Excel and SPSS to create scatterplots and measure Pearson’s Correlation.

These values listed above in the table were entered into Excel with the purpose of seeing if a correlation existed, and if there was a positive or negative trend associated with the data.

Lastly, this data was used in SPSS to measure for the Pearson’s Correlation to determine what kind of correlation, positive or negative, and how strong it was.

The two data sets have a -0.896 Correlation. This number means there is a very strong negative correlation, suggesting as distance away from the sound source increases, decibel level decreases.

SPSS can also be used to create a correlation matrix, which takes all the variables you are testing, and compares them to one another. We used basic Detroit Census data and found strong relations ( + 0.6) existed between;

            White and Black residents (negative)
            White and having a Bachelor’s Degree (Positive)
            Median Household income and Bachelor’s Degree (Positive)
            Median Home value and Median Household income (Positive)

Part II

INTRODUCTION

The Texas Election Commission (TEC) is curious about the democratic voter breakdown from the 1980 and 2012 Presidential Elections. The TEC wants someone who is capable of analyzing the voting patterns across the state as well as voter turnout. With this the TEC is hoping to be able to identify voting patterns and clusters throughout the state.

METHODOLOGY

Once all the data has been gathered and entered correctly into a shapefile in ArcMap, the next step is to open that shapefile up into Geoda and begin running spatial autocorrelation tests on it. These tests have to be weighted, and for that we just used the standard settings for the Poly ID field. Spatial Autocorrelation tests the individual counties in either rook or queen style testing. Rook uses the counties above, below and side to side for analysis, while the queen style uses all the touching counties.

Two types of tests will be run on the data, the first being Moran’s I and the second being LISA Maps (Local Indicators of Spatial Association). Moran’s I measures “randomness” amongst the data. Using areas next to each other, Moran’s I describes the spatial autocorrelation differences amongst several geographies. Other major uses this method has, tests for difference in dialect in certain places. LISA Maps use the same data but this time produce a map. The maps will show 4 different colors, Dark Red, Light Red, Light Blue, and Dark Blue. The colors represent, High to High, High to Low, Low to High and Low to Low respectfully.

RESULTS

In this map we see several blue counties in the northeastern portion of Texas and several red counties in the south. This is showing that the 1980’s election (Democratic Votes) was high in the south and several counties were low democratic voting in the north. The graph shows a semi strong trend going in the positive direction for the 1980’s Democratic Presidential Election Data.

In this map we see similar data, blue counties in the north, not as many as in 1980, and we also see more red counties appearing in the southern portion and now western portion of the state. This data is showing the 2012 Democratic Votes for Texas. The graph shows an even higher positive trend for the data, nearly .7 in the positive direction.

This data showed us a wide variety of counties, with very little trends, except in the northern portion of the state. Percentage of people of Hispanic decent throughout Texas shows the north is mostly counties of little to no Hispanic people, and the counties in the south near the border are more likely to be Hispanic. The graph shows very little positive trend and is very spread out, may have to look back into it to see if it was done correctly.

The 1980’s voter turnout in Texas showed high numbers in the north and low numbers in the south. The red counties indicate the high to high counties and blue indicate the low to low. The graph shows a positive trend line around .46. Most counties with the exception to the eastern and central red and blue counties are generally grouped up.

The 2012 voter turnout in Texas looks similar in the southern portion of the state when compared to the 1980’s map, but that is where the similarities stop. The counties which were once red in 1980 have diminished or even turned blue. The Moran’s I chart shows it at a 0.33, which is .13 lower than the 1980 voter turnout.

CONCLUSION

When looking at the 5 maps we see several trends. One major trend which stuck out was the Hispanic population in Texas, mostly found in the south according to the data, showed little voter turnout when compared to the population, but the voters who did show up showed strong democratic voting patterns. The state is fairly split when it comes to voting democratic or not. Based on just using the maps, and not including prior knowledge I would say that northern Texas is prominently white republican voters, while the south is Hispanic democratic voters. Lastly, adding on to that the maps are showing that voter turnout is increasing greatly in the south and decreasing in the north.

The people at TEC have been given some great information about what kind of trends are going on throughout the state, and if given more data or possibly more in depth data results and trend patterns could become more definite. Possibly even using regression analysis or hot spot identification would lead to more accurate data trend finding.

In this lab we used several different tools of correlation through different computer softwares.
Overall the tools are a great way to see if any features are related to one another and how strong of
a relationship the features have together. These tools have many real world purposes, calculating
trends in voting patterns is just one of many applications statistical analysis may have in a real world
situation.