Lab 4: Correlation and Spatial Autocorrelation

Correlation

In order to measure if there is any correlation between the distances someone is away from the sound source and the level of the sound measured in decibels (dB) there are tools in both Microsoft Excel and SPSS to create scatterplots and measure Pearson’s Correlation.

These values listed above in the table were entered into Excel with the purpose of seeing if a correlation existed, and if there was a positive or negative trend associated with the data.

Lastly, this data was used in SPSS to measure for the Pearson’s Correlation to determine what kind of correlation, positive or negative, and how strong it was.

The two data sets have a -0.896 Correlation. This number means there is a very strong negative correlation, suggesting as distance away from the sound source increases, decibel level decreases.

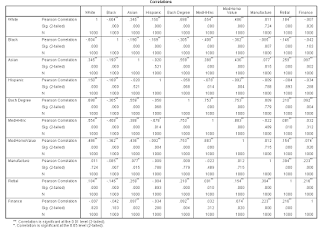
SPSS can also be used to create a correlation matrix, which takes all the variables you are testing, and compares them to one another. We used basic Detroit Census data and found strong relations ( + 0.6) existed between;

            White and Black residents (negative)
            White and having a Bachelor’s Degree (Positive)
            Median Household income and Bachelor’s Degree (Positive)
            Median Home value and Median Household income (Positive)

Part II

INTRODUCTION

The Texas Election Commission (TEC) is curious about the democratic voter breakdown from the 1980 and 2012 Presidential Elections. The TEC wants someone who is capable of analyzing the voting patterns across the state as well as voter turnout. With this the TEC is hoping to be able to identify voting patterns and clusters throughout the state.

METHODOLOGY

Once all the data has been gathered and entered correctly into a shapefile in ArcMap, the next step is to open that shapefile up into Geoda and begin running spatial autocorrelation tests on it. These tests have to be weighted, and for that we just used the standard settings for the Poly ID field. Spatial Autocorrelation tests the individual counties in either rook or queen style testing. Rook uses the counties above, below and side to side for analysis, while the queen style uses all the touching counties.

Two types of tests will be run on the data, the first being Moran’s I and the second being LISA Maps (Local Indicators of Spatial Association). Moran’s I measures “randomness” amongst the data. Using areas next to each other, Moran’s I describes the spatial autocorrelation differences amongst several geographies. Other major uses this method has, tests for difference in dialect in certain places. LISA Maps use the same data but this time produce a map. The maps will show 4 different colors, Dark Red, Light Red, Light Blue, and Dark Blue. The colors represent, High to High, High to Low, Low to High and Low to Low respectfully.

RESULTS

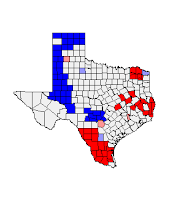
In this map we see several blue counties in the northeastern portion of Texas and several red counties in the south. This is showing that the 1980’s election (Democratic Votes) was high in the south and several counties were low democratic voting in the north. The graph shows a semi strong trend going in the positive direction for the 1980’s Democratic Presidential Election Data.

In this map we see similar data, blue counties in the north, not as many as in 1980, and we also see more red counties appearing in the southern portion and now western portion of the state. This data is showing the 2012 Democratic Votes for Texas. The graph shows an even higher positive trend for the data, nearly .7 in the positive direction.

This data showed us a wide variety of counties, with very little trends, except in the northern portion of the state. Percentage of people of Hispanic decent throughout Texas shows the north is mostly counties of little to no Hispanic people, and the counties in the south near the border are more likely to be Hispanic. The graph shows very little positive trend and is very spread out, may have to look back into it to see if it was done correctly.

The 1980’s voter turnout in Texas showed high numbers in the north and low numbers in the south. The red counties indicate the high to high counties and blue indicate the low to low. The graph shows a positive trend line around .46. Most counties with the exception to the eastern and central red and blue counties are generally grouped up.

The 2012 voter turnout in Texas looks similar in the southern portion of the state when compared to the 1980’s map, but that is where the similarities stop. The counties which were once red in 1980 have diminished or even turned blue. The Moran’s I chart shows it at a 0.33, which is .13 lower than the 1980 voter turnout.

CONCLUSION

When looking at the 5 maps we see several trends. One major trend which stuck out was the Hispanic population in Texas, mostly found in the south according to the data, showed little voter turnout when compared to the population, but the voters who did show up showed strong democratic voting patterns. The state is fairly split when it comes to voting democratic or not. Based on just using the maps, and not including prior knowledge I would say that northern Texas is prominently white republican voters, while the south is Hispanic democratic voters. Lastly, adding on to that the maps are showing that voter turnout is increasing greatly in the south and decreasing in the north.

The people at TEC have been given some great information about what kind of trends are going on throughout the state, and if given more data or possibly more in depth data results and trend patterns could become more definite. Possibly even using regression analysis or hot spot identification would lead to more accurate data trend finding.

In this lab we used several different tools of correlation through different computer softwares.
Overall the tools are a great way to see if any features are related to one another and how strong of
a relationship the features have together. These tools have many real world purposes, calculating
trends in voting patterns is just one of many applications statistical analysis may have in a real world
situation.